Overview
See Changes, flows, growth rates. Amounts outstanding ('levels') data on the other hand, are usually not adjusted for breaks in this way.
See Changes, flows, growth rates. Amounts outstanding ('levels') data on the other hand, are usually not adjusted for breaks in this way.
These Explanatory notes use the term break-adjusted to relate to amounts outstanding (levels) data series constructed to be consistent with transactions (flows) and growth rates data. The term break-adjusted is not applied to flows and growth rates data, as it is understood that these data, by definition, incorporate any adjustments required to offset the impacts of breaks.
With the exception of a limited number of high profile monetary aggregates series, the Bank of England does not routinely publish data for break-adjusted levels series. Other than for these exceptions, Bank of England published levels data should be understood to be non-break-adjusted. One reason for this approach is to avoid a potential source of confusion to users, given that any break-adjusted levels series can be arbitrarily scaled. Data users can, however, readily construct break-adjusted series consistent with the published data for themselves. This is explained below.
Break-adjusted levels data can be constructed by fixing the level for any arbitrarily chosen reference period, and recursively dividing (or multiplying) by one-period growth rate factors to generate values for all other periods in the range of interest, before (or after), the reference period. The growth rate factor is determined from the flow during the period and the amount outstanding at the previous period. One option is to choose the reference period to represent the latest published data point. In this case, the break-adjusted amount outstanding in the reference period is the value of the published amount outstanding, and levels for all preceding periods are calculated by successively dividing by the growth rate factors. Another approach can be to choose a historic reference period and to take the published value for that period, or to set it to 100 in order to create break-adjusted series in index form, and then to apply growth rate factors to subsequent and preceding periods as appropriate.
If break-adjusted versions of both seasonally-adjusted (SA) and non-seasonally adjusted (NSA) forms of a data series are to be constructed, users may wish to ensure that seasonal adjustment factors are preserved in the constructed series (or index). To do this, it is sufficient to constrain the reference period values of the break-adjusted SA and NSA series to be the corresponding values of the published data in that period.
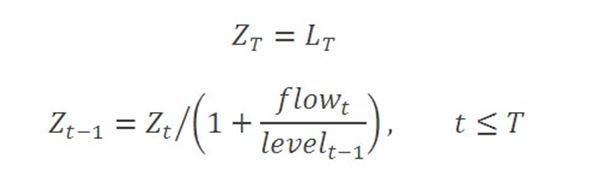
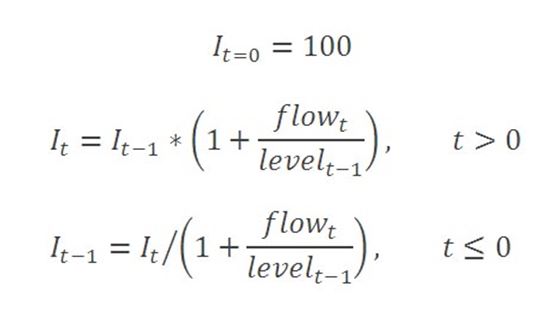
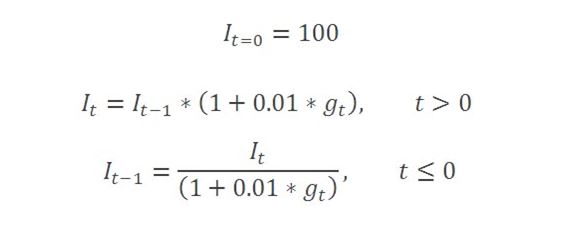
These calculations are illustrated in spreadsheet format in this worked example.
It is assumed that OCVA effects are non-seasonal in nature, so that seasonally adjusted levels data should contain the same breaks as their non-seasonally adjusted counterparts. Break-adjustment of levels data is conducted as the first stage in the process of seasonal adjustment of levels data, and the reverse process is applied as the final stage. This procedure ensures that the resulting seasonally adjusted series reflects the same underlying OCVA effects as the non-seasonally adjusted series and that the flows (transactions) and growth rates of these data are free of any distortions that might be caused by breaks in the levels data. See Explanatory notes on Seasonal adjustment.
Published break-adjusted levels series are available on the Interactive Database for a limited number of monetary aggregates. These are calculated so as to be constrained to the published data for the latest period.